Área bajo la curva mediante suma de rectangulos: La función seno.
Antes de sumergirnos en el problema sugiero una lectura a la primera sección del capitulo 12 del libro Análisis matemático de Hasser, La Salle, Sullivan.
También me gustaría recalcar que estrictamente hablando, no estoy utilizando las Sumas de Riemann.
Una vez dicho esto, comencemos.
Sea  una función acotada tal que
una función acotada tal que  , nos daremos a la tarea de hallar el área acotada por la función y el eje x mediante la suma de rectangulos contenidos entre estos dos .
, nos daremos a la tarea de hallar el área acotada por la función y el eje x mediante la suma de rectangulos contenidos entre estos dos .
Sabamos de antemano que  es una función actotada entre [0,1] por lo que es continua en todo punto de su dominio.
es una función actotada entre [0,1] por lo que es continua en todo punto de su dominio.
Para empezar, proponemos la partición regular , donde
, donde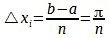 y
y  . Entonces definimos el área como
. Entonces definimos el área como que no es otra cosa que la suma de n rectángulos de base Δx y altura f(x¡)
que no es otra cosa que la suma de n rectángulos de base Δx y altura f(x¡)

Con el fin de ahorrarnos un par de caracteres y facilitar la resolución del problema, haremos a θ = π/n de tal forma que la suma sea

Ahora solo tenemos que resolver la suma para dejarla unicamente en terminos de n, para lo cual utilizaremos la identidad trigonométrica  estableciendo a x= θi y y=θ/2 (esto lo hacemos ya que la identidad trigonométrica lo permite y porque necesitamos un valor para desarrollarla en términos mas simples). Luego
estableciendo a x= θi y y=θ/2 (esto lo hacemos ya que la identidad trigonométrica lo permite y porque necesitamos un valor para desarrollarla en términos mas simples). Luego


Reescribiendo la suma
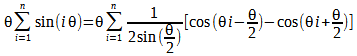

La suma ahora tiene una expresión de la forma 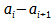 , establecemos entonces
, establecemos entonces  . Entonces
. Entonces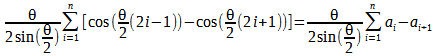
 Por convergencia de sumas telescópicas.
Por convergencia de sumas telescópicas.

Trabajando con el segundo coseno tenemos
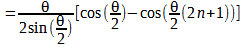




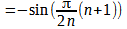

Así, la igualdad original es reescrita de la siguiente manera
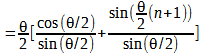
 Por transitividad.
Por transitividad.
El área bajo la curva está definida por 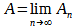 , pero como
, pero como , necesitamos hacer el cambio de limite a
, necesitamos hacer el cambio de limite a 
Por lo que nuestra definición de área resulta en 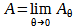 . Entonces
. Entonces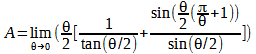
 Todos son límites conocidos
Todos son límites conocidos

Por lo que podemos concluir que el área acotada por la función y el eje x es 2.
Es fácil comprobar el resultado usando las formulas de integración, sin embargo aqui lo haremos haciendo uso de python, pero como no es el objetivo del post no explicare el código.
Adjunto un video dónde se explica como se construye la suma para la función seno.
Comentarios
Publicar un comentario